(Aug 9, 2022)
This document is about understanding a special token in Web3 called Stablecoins. We posit one central idea - the collateral ratio has a dominant influence on the behavioral economics of Stablecoins. We first describe them and highlight the core attributes of a few variants. We then pose a simple model asking what happens when an outside force introduces downward price pressure on them. That model illuminates how the collateral ratio determines a lot of the game theoretic behavior. We close by asking three important questions.
We think this document is accessible to everyone.
Stablecoins?
Stablecoins are tokens meant to always trade at par with an external quantity. This is often the US dollar and we assume that for the rest of this document. The most popular ones are USDT, USDC, and DAI, with the following distinguishing attributes:
- USDT is the oldest (2014) and biggest in terms of volume. It claims to be fully collateralized, although many assume it to be vastly undercollateralized.
- USDC was started by the Coinbase / Circle consortium, two American companies whose business value depends on the American government liking them. It is 100% collateralized by the US dollar and the consortium publishes reports attesting to this.
- DAI is an Algorithmic Stablecoin. It strives to be backed 150% by blue chip tokens (ETH, BTC, USDC, etc). Borrowers put up $1.50 in collateral and pay a coupon to borrow $1 of DAI. When they return the $1, they get back their collateral after deducting the coupon. The protocol controls demand for borrowing through the coupon rates. By increasing (decreasing) the rate, they attract fewer (more) borrowers. There is also an option to loan your DAI to the system, the flip side to borrowing DAI. Together, these mechanisms keep DAI pegged at $1.. If DAI is above (below) $1, then there is a surplus (deficit) of demand for it, and more DAI needs to be minted (burned) to return the price to $1, so the rates are pushed to be more (less) attractive to borrow.
USDC offers no incentives to holders because it is 100% collateralized from the start and this remains invariant. It is a safe option. Because DAI is algorithmic, it needs to incentivize people to collateralize it when supply is low and remove collateral when supply is high. To do this, as suggested above, it offers a return on capital.
As of July 27th, 2022, there is $7.3bn DAI outstanding, collateralized by $9.8bn in locked collateral made up of a range of different coins (USDC, BTC, ETH, MANA, YFI, LINK, etc). The collateral ratio is less than 150% because the recent crypto market downturn caused a drop in the value of the held collateral.
Users lock up their collateral for DAI because they are attracted to the terms of the loan. Users lock up their DAI for others to borrow because they earn a suitable return on that staked capital.
More on Algorithmic Stablecoins.
Vitalik Buterin’s Stablecoin post has a succinct part on Algorithmic Stablecoins that introduces the concept of a Volcoin. We liberally borrow that here:
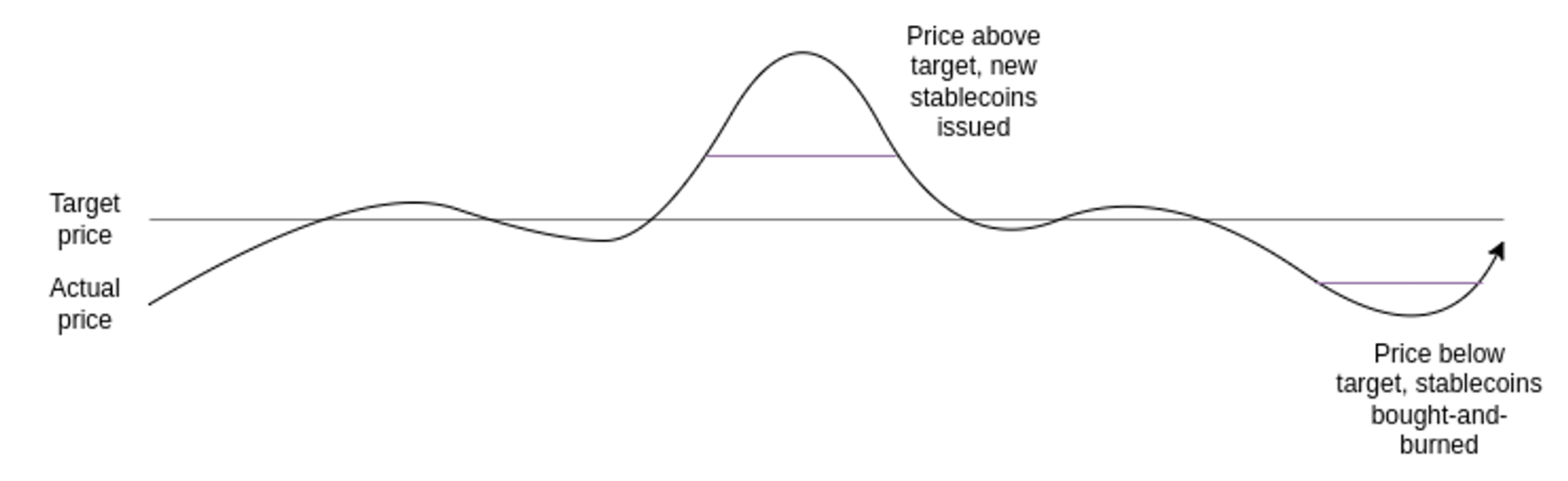
The Stablecoin retains stability using a simple mechanism:
- If the price of the Stablecoin exceeds the target, the system auctions off new Stablecoins (and uses the revenue to burn Volcoins) until the price returns to the target.
- If the price of the Stablecoin drops below the target, the system buys back and burns Stablecoins (issuing new Volcoins to fund the burn) until the price returns to the target.
Now what is the price of the Volcoin? The Volcoin's value could be purely speculative, backed by an assumption of greater Stablecoin demand in the future (which would require burning Volcoins to issue). Alternatively, the value could come from fees: either trading fees on Stablecoin <-> Volcoin exchange, or holding fees charged per year to Stablecoin holders, or both. But in all cases, the price of the Volcoin comes from the expectation of future activity in the system.
Under-collateralized Stablecoins.
USDC, USDT, and DAI all claim to be fully or over-collateralized. We want a Stablecoin that is under-collateralized to better lubricate the economy. This is a similar concept to the reserve ratio countries used on the gold standard. There was a hard asset, gold, backing a currency according to an expected, if not required, minimum ratio. Here, the hard asset is USD (at least by consensus) backing a Stablecoin according to an expected, if not required, minimum ratio. Requiring a government to keep 99% of deposits in reserve inhibits loan-making. Reducing that reserve ratio requirement to 90% or 50% frees up the money to juice the economy. However, it also makes the system more susceptible to calamitous effects when those loans default. Ideally, we’d expand and retract the rate to ensure the system is healthy, similar to how DAI has its levers. Today, the Federal Reserve Bank operates this lever with the American Dollar.
Overall, we seek a Stablecoin that a) keeps its peg to $1 most of the time, b) never deviates by more than a marginal amount, and c) is under-collateralized. This is not new - crypto protocols have explored many designs involving a Volcoin. Taking this to a limit where there is no starting collateral was Luna’s infamous approach.
Modeling Stablecoins.
Assume a collateral ratio of CR representing the amount of required USD backing for the Stablecoin. Here are a couple of examples:
- In Luna, Stablecoin = UST, Volcoin = Luna, and the CR = 0. Users were incentivized to hold Luna because its price was mooning, to hold UST because they could deposit in Anchor for a ~19% return, and to maintain the peg for short-term arbitrage returns.
- For USDC, Stablecoin = USDC, CR = 1, and there is no Volcoin because it’s backed by actual US dollars. There is no Volcoin / Stablecoin swap mechanism, but instead guaranteed exchange of fiat currency. Users are not incentivized to hold USDC but do so because it a guaranteed low-volatility backed token where they can park assets in between investments.
Imagine that an exogenous event, say a profit-seeking market participant executing a daring trade, “punched” USDC’s price below $1. It will quickly recover because it is fully collateralized. That was not true of Luna; when UST was punched hard enough, the whole system collapsed due to insufficient collateralization.
It’s impossible to model this punching without building an order book, but building that requires having some idea of what sellers and buyers will do, akin to modeling all of the inputs.
You can skip this, but here’s a brief interlude to define terms used in other callouts. Say there’s an initial price and quantity of Volcoin (P_v, Q_v) and similar for Stablecoin (1, Q_s). We have Sellers S_i and buyers B_i. Each Seller has a function determining its contribution to the order book f_S: (P_v, Q_v, Q_s) → (quantity, ask) and each Buyer has similarly an f_B: (P_v, Q_v, Q_s) → (quantity, buy).
If we could model buyers and sellers, we would first simulate punching the Stablecoin price below $1. Then we would sequentially simulate the result, building and completing the order book at each step. Each run will be a single simulation. Aggregate all of these runs as data to answer questions about how the collateral ratio affects the result.
That would be charming, wouldn’t it?
There are two immediate problems:
- Whatever it is that models the buyers and sellers actually depends on the CR as well. People change the way they operate if CR is 1.0 vs 0.9 vs 0.2. So we can’t just keep the modeling constant, change the CR, and expect the results to be scientifically meaningful.
- “Modeling buyers and sellers” hides an enormous amount of complexity governing behavioral economics at large. In a bank run, which is roughly what we are modeling, buyers and sellers could exhibit any of a wide family of preferences in how they operate. How would we decide what preference to use? This is not constrained enough.
The first problem above is saying that f_S and f_B also take CR as an input.
The second problem is saying that, to a first order, the only rule we are requiring for our f_S and f_B is that at CR = 0.0, it must be possible for the value of P_v and P_s to go to zero and at CR = 1.0, P_s must return to 1. Consequently, f_S and f_B are ill-constrained.
The role of Interest Rates
Before we examine in more detail the role of the Collateral Ratio, it’s important to think about the comparable role of interest rates. Recall that in DAI the CR is pegged at 150%, and it is the interest rate lever that moves up and down in order to manage the stability. This is how traditional finance works as well. Organizations, including the Federal Reserve Bank, will generally leave CRs fixed and adjust interest rates to manage lending and risk taking.
When we declare a CR < 1, we are declaring that capital needs to be injected into the system in some way in order to make up the difference; it can’t be made from nothing. Another interpretation is that we are somewhere taking in a loan of capital and giving a rate of return on that loan. In other words, we are implicitly describing lending with a positive interest rate. We don’t expand on this here, but an interesting question is whether it’s better to have levers for manipulating the CR or the IR. This is a key difference between DAI and another competing Stablecoin protocol - FRAX.
Examining different Collateral Ratio levels.
Let’s start by considering if the CR was slightly less than 1, say CR = 0.99. In that case, punching the Stablecoin to $0.95 would be a non-issue because there is publicly verifiable collateral at $0.99, and so panic would be minimal. Some enterprising people will buy more to arbitrage trading in their tokens for the collateral.
What if the CR = 0.90? Then a punch to $0.95 would also correct itself via arbitrage. There are two differences though between this and the CR = 0.99 case.
- More Volcoin is required to return the price to $1. Due to the lower CR, we need to correspondingly mint more Volcoin on each arbitrage, and so Volcoin would decrease in price by more than if the CR = 0.99.
- Holders will be more skittish. How much more skittish? Say some very skittish subset sold their stakes. Because the collateral is there, the price should dip below $0.90 by only negligible amounts. After $0.89, a buy wall would arise to capture the free arbitrage given that the price of USD, the collateral, is not affected. We expect this 10% short-term paper loss to recapitalize without issue.
What happens if the CR is very low, say CR = 0.20, and the Stablecoin was punched? Participants would know that the Stablecoin price could precipitously drop to $0.20, low enough that a dash to exit would ensue and consequently mint a lot more Volcoin. While Stablecoin would remain above $0.20 because of the CR, Volcoin could easily → $0. It can do this for two reasons:
- Volcoin’s market cap is much less than Stablecoin’s market cap and so too much Volcoin has to be minted to return Stablecoin to $1.
- If faith in Stablecoin suffers too much, a death spiral could ensue if the public perceives that Stablecoin will not be stable at $1 in the future. As long as Stablecoin remains in the $0.20 - $0.30 range, arbitrageurs will act but then immediately sell Volcoin (for profit) because they don’t actually know whether Volcoin will persist. This inflates Volcoin quantity, reduces its price even more, and leads to a death spiral as ever higher quantities are needed to bring Stablecoin back to $1. Consequently, Stablecoin will be difficult to recapitalize without Volcoin → $0.
Can this be avoided outside of maintaining a high collateral ratio like in DAI? Yes. One way is to create cash flows to Volcoin exogenous to the system, which equips the DAO with the ability to be a buyer of last resort and makes the system more robust. Another way is to use the token as the base coin to transact in a real economic system. This is “sovereignty” and participants’ demand makes them the buyers supporting the token’s price stability.
Regardless if Volcoin → 0, if the CR = 0.80, then Stablecoin will settle at minimum $0.80. It may actually rise again to $1 if there is enough value in the remaining Volcoin to operate the arbitrage. A quick sketch of that begins with $1bn in Volcoin (10m each priced at $100) and $1bn in Stablecoin. Now punch Stablecoin to $0.80 - there’s now 1bn with a market cap of $800m. To a first order approximation, to make this stable again, we need to:
- Buy 200m Stablecoin for $160m of USD.
- Use the two-sided mechanism to burn that for $160m of USD and $40m of Volcoin = 400k Volcoin. This arbitrageur is net even USD and up 400k Volcoin.
- Globally, we now have less 200m Stablecoin in the system for a total of 800m at a market cap of $800m = $1 each. We also now have an extra 400k Volcoin for a global total of 10.4m at $96.15 each.
- The abitrageur can then sell this 400k Volcoin for a large gain.
What the Collateral Ratio is actually modeling.
The resulting price doesn’t suffer much when CR = 0.8 because the CR is so high. When the CR = 0, like it was in Luna, the game theoretic optimum price can easily be $0 following an exogenous shock. That clues us in to the CR having an outsized influence on how market participants behave.
At 0.99, it may as well be 1 because people don’t change their actions for that .01 knowing that it will go up again from arbitrage. At 0.90, they’ll check the contract to ensure that the backing is real. At 0.20, they’re going to sell first and fast to get out above $0.20.
Three questions arise from this. We write them below and leave them for future work. Reach out if you’re interested in tackling one of these with us:
- What happens if the CR is responsive? What adversarial games can be played when you have a CR that isn’t fixed but changes according to some set of predictable market movements? What behaviors do we get when the CR has a reflexive affect on market participant actions? This is how FRAX & FXS work and will be covered in the next release.
- With respect to market confidence, what does the CR curve look like? We expect there to be a precipitous drop in confidence at some point. This is because we know it won’t work at 0 (see Luna), have strong believe it won’t work at 0.2, have shaky belief it will work at 0.8, and know it will work at 1. FRAX is empirical evidence that the market is satisfied at 0.82 and considers 0.9 a return to safety. Could a stablecoin consistently operate with a CR less than 0.8 or is that a “confidence minimum”?
- How fast can the system recollateralize? Recollateralizing after a big shock is akin to convincing enough market participants that this asset is severely undervalued and will come back, so why don’t you pick up the arbitrage and help us bring it back? That’s true whether it’s a large whale doing it (Warren Buffet and the banks in 2008) or a lot of smaller retail participants deciding that actually this is ok now. How would the FRAX core team answer this?
